Wilson current mirror

A Wilson current mirror or Wilson current source is a circuit configuration designed to provide a constant current source or sink. It is named after George Wilson, an integrated circuit design engineer working for Tektronix.[1] Rumor has it that Wilson came up with this configuration after being challenged by Barrie Gilbert to come up with a useful new circuit that used three active devices.

Contents

Circuit Analysis

Assumptions:

  1. All transistors have the same current gain β.
  2. Q1 and Q2 are matched, so their collector currents are equal.

Therefore, IC1 = IC2 (= IC) and IB1 = IB2 (= IB) ... (1)

Base current of Q3 is given by,

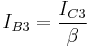I_{B3} = \frac{I_{C3}}{\beta} ... (2)

and emitter current by,

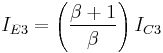I_{E3} = \left(\frac{\beta %2B 1}{\beta}\right)I_{C3} ... (3)

From the schematic, it is evident that IE3 = IC2 + IB1 + IB2 ... (4)

substituting for IC2, IB1 and IB2 from (1) in (4),

IE3 = IC + 2.IB ... (5)

so,

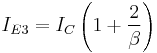I_{E3} = I_C\left(1 %2B \frac{2}{\beta}\right) ... (6)

substituting for IE3 from (3),

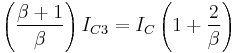
\left(\frac{\beta %2B 1}{\beta}\right)I_{C3} = I_C\left(1 %2B \frac{2}{\beta}\right)

rearranging,

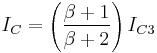I_C = \left(\frac{\beta %2B 1}{\beta %2B 2}\right)I_{C3} ... (7)

Current through R1 is given by,

IR1 = IC1 + IB3 ... (8)

But, IC1 = IC2 = IC

Substituting for IC from (7) in (8) and since 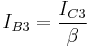I_{B3} = \frac{I_{C3}}{\beta} we get,

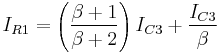I_{R1} = \left(\frac{\beta %2B 1}{\beta %2B 2}\right)I_{C3} %2B \frac{I_{C3}}{\beta} ... (9)

Therefore, 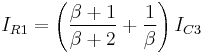I_{R1} = \left(\frac{\beta %2B 1}{\beta %2B 2} %2B \frac{1}{\beta}\right)I_{C3} ... (10)

And finally,

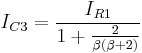I_{C3} = \frac{I_{R1}}{1 %2B \frac{2}{\beta(\beta %2B 2)}} ... (11)

From the above equation we can see that if 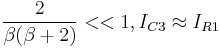\frac{2}{\beta(\beta %2B 2)} << 1, I_{C3} \approx I_{R1}

And the output current (assuming the base-emitter voltage of all transistors to be 0.7 V) is calculated as,

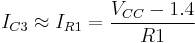
I_{C3} \approx I_{R1} = \frac{V_{CC} - 1.4}{R1}

The output current is thus substantially dependent only on VCC and R1 and the circuit acts as a constant current source; that is, the current remains constant with variations in load. However, variations in VCC will be reflected in variations in the output current.

Advantages over other configurations

This circuit has the advantage of virtually eliminating the base current mis-match of the conventional current mirror thereby ensuring that the output current IC3 is almost equal to the reference or input current IR1. It also has a very high output impedance.

Further improvement

Adding a fourth transistor to the Wilson current mirror (as shown in the diagram to the right) improves its linearity at higher current levels. It accomplishes this by equalizing the collector voltages of Q1 and Q2 at 1 Vbe. This leaves the finite beta and voltage differences of each of Q1 and Q2 as the remaining unbalancing influences in the mirror.[2]

Furthermore, the power dissipated in the junctions of Q1 and Q2 will be close to the same which tends to cancel the thermal effects on Vbe.


References

  1. ^ Sedra, A.S. & Smith, K.C.: "Microelectronic Circuits, 5th Ed.", page 651. OUP, 2006
  2. ^ B. Wilson, Current mirrors, amplifiers and dumpers, Wireless World, December, 1981 p. 47, at p. 48. The author was, at the time of the article, a Ph.D. in the Department of Instrumentation and Analytical Science, University of Manchester Institute of Science and Technology.

See also